Fuzzy rectangle
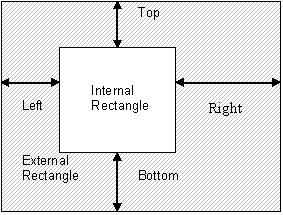
Fuzzy rectangle is a structure that describes a class of rectangles whose boundaries lie within specific allowed ranges. A fuzzy rectangle consists of two rectangles – an external rectangle and an internal rectangle.
In the FlexiLayout language, fuzzy rectangles are represented by type FuzzyRect.
As can be seen in Figure below, in the general case, when constraints for all the boundaries are set, there is a part of the search area that must fall within any hypothesis for the element. It is this part that forms the internal rectangle. The maximum-size circumscribing rectangle of the possible hypothesis forms the external rectangle.
Show me...
Let the boundaries of the element be:
LeftBound: [L1, L2], where L1 <= L2
TopBound: [T1, T2], where T1 <= T2
RightBound: [R1, R2], where R1 <= R2
BottomBound: [B1, B2], where B1 <= B2
Then the fuzzy rectangle containing the information about the specified boundaries will be formed as follows: InternalRect: [L2, T2, R1, B1], ExternalRect: [L1, T1, R2, B2].
If the user sets no constraints for the boundaries of the search area, the internal rectangle degenerates and makes no geometrical sense. In this case L1=R1, L2=R2, T1=B1, T2=B2.
Suppose now that no constraints have been specified for the search area. Then, if the maximum and minimum allowed number of pages is 1, the fuzzy rectangle of the search area will be created as follows:
LeftBound: [PageRect.Left, PageRect.Right]
TopBound: [PageRect.Top, PageRect.Bottom]
RightBound: [PageRect.Left, PageRect.Right]
BottomBound: [PageRect.Top, PageRect.Bottom]
InternalRect: [PageRect.Right, PageRect.Bottom, PageRect.Left, PageRect.Top]
ExternalRect: [PageRect.Left, PageRect.Top, PageRect.Right, PageRect.Bottom]
and in the case of a multi-page document:
LeftBound: [-INF, INF]
TopBound: [-INF, INF]
RightBound: [-INF, INF]
BottomBound: [-INF, INF]
InternalRect: [INF, INF, -INF, -INF]
ExternalRect: [-INF, -INF, INF, INF]
As can be seen from the above expressions, the external rectangle coincides with the rectangle of the entire page, and the internal rectangle degenerates and has negative height and width.
Fuzzy rectangles can be united and intersected. When two fuzzy rectangles are intersected, their corresponding boundaries intersect: the right boundary of one rectangle intersects with the right boundary of the other, the left with the left, etc. This creates new ranges for the boundaries:
LeftBound: [L1’, L2’]
TopBound: [T1’, T2’]
RightBound: [R1’, R2’]
BottomBound: [B1’, B2’]
The resulting fuzzy rectangle will be created using the resulting intervals: InternalRect: [L2’, T2’, R1’, B1’], ExternalRect: [L1’, T1’, R2’, B2’].
If, as a result of the intersection, at least one of the conditions for creating the fuzzy rectangle (L1 <= L2, T1 <= T2, R1 <= R2, B1 <= B2) is not met, the resulting fuzzy rectangle will be nullified: InternalRect: [0, 0, 0, 0], ExternalRect: [0, 0, 0, 0]. Usually an empty fuzzy rectangle is created as a result of contradictory conditions, e.g. if you attempt to intersect two fuzzy rectangles whose external boundaries do not intersect.
Fuzzy rectangles are united in the same way: first, the ranges of each boundary are united. As a result of uniting the two ranges, a minimum range is created which contains both specified ranges. After the boundaries have been united, a new fuzzy rectangle is formed.
In practice you will most often encounter fuzzy rectangles with a degenerated internal rectangle. Only on rare occasions will you need to set constraints on a specific boundary. However, the search area for an element is always represented by a fuzzy rectangle and an array of excluded rectangles.
12.04.2024 18:16:02